本記事では,インデックス投資家の多くの方が興味がある利回り計算のためのシミュレーションツールを紹介しています.シミュレーションツールを作るにあたって利回り計算を求められるようにするための計算方法についても紹介しています.
シミュレーションツール開発の背景
インデックス投資家の方は大勢いらっしゃると思います。日本でインデックス投資を行うには、以下の2種類が代表的です。
- ETF
- 投資信託
どちらに投資するか悩まれている方は多いと思います。
例えばS&P500指数では、以下のような選択肢があります。
| 種類 | 銘柄例 |
|---|---|
| 投資信託 | eMAXIS Slim米国株式(S&P500) SBIバンガード S&P500 インデックス ファンド |
| ETF | VOO SPY IVV |
これらの比較の際に、一般的な投資信託やETF商品のメリット・デメリットはもちろんありますが、やはりパフォーマンスの差は重要です。
パフォーマンスは、株式上昇率や配当率だけではなく、以下のような要素も関係してきます。
- ファンド経費
- 配当金にかかる税金
- 株式売却時にかかる税金
- 為替手数料
- 約定手数料
これらを全て加味したトータルパフォーマンスを計算しないことには比較することが出来ません。しかし、これらのトータルパフォーマンスの計算について述べている文献は見つかりませんでした。そこで、トータルパフォーマンスの検証が容易になるように、解析的に計算を可能にするための公式を導きました。
また、誰でも簡単に計算出来るように、シミュレーション用のExcelもダウンロード可能です。
このページでは、以下の2点を紹介します。
- 投資信託とETFのパフォーマンス検証のための公式
- シミュレーション用のExcel
投資信託とETFの数理モデルと公式の特徴
- 公式は、一般的なETFと分配金抑制型の投資信託に適用できます。
- 一括投資と積立投資の両方に対応しています。
- 前提条件をおいており、現実の結果とは異なる可能性があります。
- トータルパフォーマンスの傾向を見るには十分な結果を得られると思います。
- 公式は海外ETFと投資信託に用意してあります。国内ETFは、ETFの公式で、約定手数料と米国税率を0にすれば、適用出来ます。
- 計算は慎重に行っていますが、誤っている可能性もあります。誤りを見つけた場合、コメント欄やTwitterのメッセージでご連絡ください。
Excelツールのダウンロード
ファイルは以下からダウンロード可能です。投資信託 パフォーマンスシミュレーター (配布用) v0.1.xlsx
ツールの著作権は放棄しませんが、結果は自由に引用いただいて構いません。こちらのホームページを参考にしたことを明記いただけると嬉しいです。
- 前提条件は、Excelシートにも書かれているので必ずお読みください。
- 計算結果には、責任は持てません。あくまでご参考までにご利用ください。
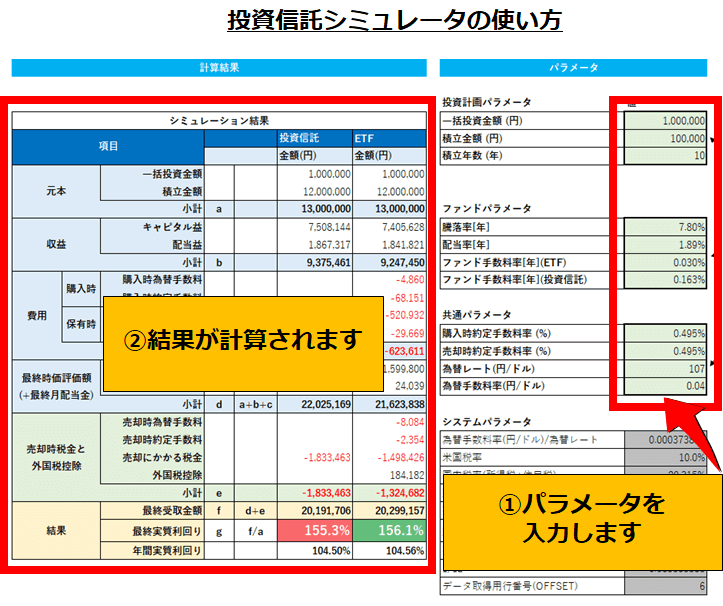
シミューレータの使い方は、以下の通りです。
- 薄緑色の枠に、パラメータを入力します。
- 自動的にシミュレーション結果が表示されます。
前提条件
投資信託とETFが従うお金の流れのモデル
投資信託とETFのそれぞれのお金の流れは、以下の記事で説明していますので、必要に応じてご確認ください。この数理モデルも、以下のお金の流れの考え方に従っているものとします。

投資計画
- 投資期間の最初の初月の一括投資と、毎月決まった額の積立投資
- 配当金は再投資
- 積立期間終了後、一括で売却
数理モデル上の制限
- 最低購入単位未満でも購入可能
- 為替レート、配当率、株価上昇率は投資期間において固定
- 配当率は月ベースに換算し、毎月配当金が発生
その他の条件
積立と配当金再投資
- 投資信託およびETFは、最低購入金額の最低購入金額を無視して購入可能
- 配当率は月当たりに換算し、毎月配当金が発生
売却
- 積立期間満了後、全ての株および投資信託を一括で売却または解約
- 海外ETF売却後は、全額をドルから円に転換
為替
- 為替レートは投資期間中固定
配当率と騰落率
- 騰落率は投資期間中固定
- 配当率は投資期間中固定
配当金
- ETF:配当金にかかった米国税は、確定申告の外国税控除で奪還
- ETF:確定申告で取り戻した配当金の米国税は再投資しない
- 投資信託:発生した配当金は米国内で課税後、自動的に再投資
パラメータ
初期パラメータは以下の記号で表します。
| パラメータ | 意味 |
|---|---|
| \(t_0\) | 一括投資金額[単位:円] |
| \(t\) | 積立金額[単位:円] |
| \(n\) | 積立月数 |
| パラメータ | 意味 |
|---|---|
| \(r\) | 騰落率[月] |
| \(d\) | 配当率[月] |
| \(e\) | ファンド経費率[月] |
| パラメータ | 意味 |
|---|---|
| \(\tau_{JP}\) | 日本国内税率 |
| \(\tau_{US}\) | 米国税率 |
| パラメータ | 意味 |
|---|---|
| \(l_{buy}\) | 購入時約定手数料率 |
| \(l_{sell}\) | 売却時約定手数料率 |
| \(l_{max}\) | 約定手数料上限[単位:円] |
| \(g\) | 為替レート[単位:円/ドル] |
| \(\epsilon\) | 為替手数料率[単位:円/ドル] |
数式簡略化のための記号の導入
数式簡略化のために、以下の記号を導入します。ここで、\(R\)は、投資信託の場合とETFの場合で異なるため、それぞれの公式を参照してください。
\alpha&=R-1\\ \\
\beta_n&=R^n-1\\ \\
\gamma_n&=\frac{\beta_n}{\alpha} \\ \\
\eta_n&=\frac{\beta_n+1}{\alpha+1} \\ \\
\mu_n&=\frac{(1+\alpha)\gamma_n -n}{\alpha}
\end{align}
投資信託のパラメータ
調整後騰落率
投資信託の公式集
投資信託の公式は以下のようになります。
期初評価額
投資元本合計
期末評価額
期初評価額合計
キャピタル益合計
ファンド経費合計
配当金額合計
配当金にかかる税金合計
Q_{n}=\tau_{US} D_n
\end{align}
購入金額合計
W_n=T_n
\]
株式売却にかかる税金合計
U_n=\tau_{JP}(M_n-W_n)
\end{align}
最終受取金額
P_n = M_n- U_n
\]
トータル実質利回り
R_n=\frac{P_n}{T_n}
\]
ETF約定手数料に関するパターンの説明
ETFでは約定手数料が発生します。約定金額に対する約定手数料率で計算できますが、上限が決まっています。この上限を超えるか、超えないかで手数料計算が変わってきます。約定手数料がかかるのは以下のタイミングです。
- 一括投資
- 積立投資(積立金額+課税後配当金再投資)
- 売却時
最初に、各タイミングでの約定手数料のパターンを分類します。
一括投資の約定手数料
\( l_0\)は上限を考慮しない一括投資時の約定手数料です。
一括投資の約定手数料は2つのパターンに分類されます。
- 一括投資の約定手数料が上限を超える場合 \( l_0 \geq l_{max} \)
- 一括投資の約定手数料が上限を超えない場合 \( l_0 < l_{max} \)
\(l_0\)は、以下で計算されます。\( l_0 = l_{buy} t_0\)
①一括投資の約定手数料が上限を超える場合 \( l_0 \geq l_{max} \)
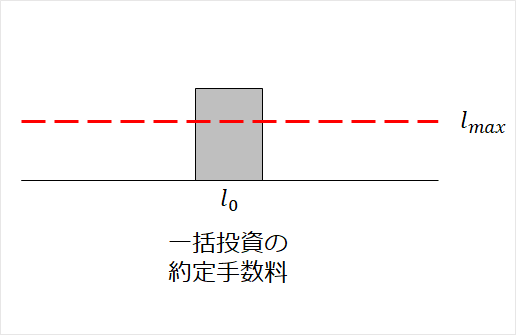
②一括投資の約定手数料が上限を超えない場合 \( l_0 < l_{max} \)

\(1 \sim n\)ヶ月目の約定手数料
\( l_1\)と\( l_n\)はそれぞれ上限を考慮しない\(1\)ヶ月目と\(n\)ヶ月目の積立投資時の約定金額です。
(参考) ETFの\(1 \sim n\)ヶ月目の約定手数料の計算
\( l_1\)と\( l_n\)は以下のように計算できます。
l_1=(1-f)t+d(1-\tau_{US})(1-\tau_{JP})(\tilde{Z}_1 – \tilde{A}_1)l
\]
l_n=(1-f)t+d(1-\tau_{US})(1-\tau_{JP})(\tilde{Z}_n – \tilde{A}_n)l
\]
ここで、\(R\), \(\tilde{A}_n\), \(\tilde{Z}_n\)はそれぞれ以下のように計算されます。
R=\lambda + d(1-\tau_{US})(1-\tau_{JP})(1-l_{buy})
\]
\tilde{A}_n=(1-f)(1-l) \eta_n t_0+ (1-f)(1-l) \gamma_n t
\]
\tilde{Z}_n=\sum_{k=1}^{n}\tilde{A}_k=(1-f)(1-l) \gamma_nt_0+ (1-f)(1-l)t \mu_n t
\]
配当金を再投資し、株価が単調に増加するモデルでは、\( l_1 < l_n\)となります。
積立投資時の約定手数料は3つのパターンに別れます。
- \(1\)ヵ月目の約定手数料が上限以上の場合 \( l_1 \geq l_{max} \)
- \(1\)ヵ月目の約定手数料は上限未満で\(n\)ヶ月目の約定手数料は上限を超える場合 \( l_1 < l_{max} < l_n\)
- \(n\)ヵ月目の約定手数料が上限以下の場合 \( l_n \leq l_{max} \)
①\(1\)ヵ月目の約定手数料が上限以上の場合 \( l_1 \geq l_{max} \)
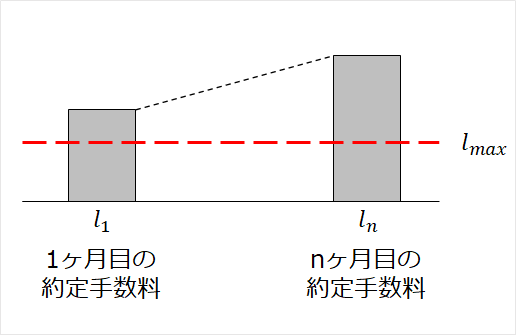
②\(1\)ヵ月目の約定手数料は上限未満だが\(n\)ヶ月目の約定手数料は上限を超える場合 \( l_1 < l_{max} < l_n\)
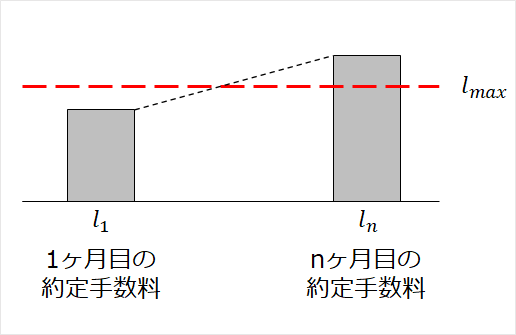
このパターンでは、解析的にはうまく表すことができません。本公式では、積立中に約定手数料が最大を超える場合であっても、約定手数料の上限をが無いものとみなして計算します。このパターンになることと、なった場合でも約定手数料が他の手数料に比べると誤差の範囲なので、このようにしています。
③ \(n\) ヵ月目の約定手数料が上限以下の場合 \( l_n \leq l_{max} \)
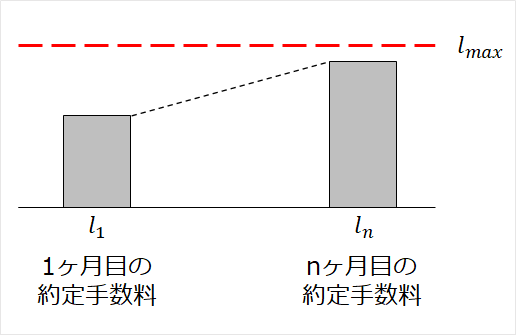
売却時約定手数料
\( l_{n(sell)} \)は上限を考慮しない売却時の約定手数料です。
売却時の約定手数料は2つのパターンに分類できます。
- 売却時の約定手数料が上限を超える場合 \( l_{n(sell)} \geq l_{max} \)
- 売却時の約定手数料が上限を超えない場合 \( l_{n(sell)} < l_{max} \)
\( l_{n(sell)} \)は、以下で計算されます。\(l_{n(sell)} = l_{sell} M_n\)
①売却時の約定手数料が上限を超える場合 \( l_{n(sell)} \geq l_{max} \)
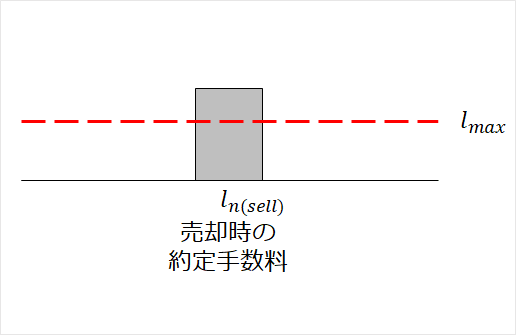
②売却時の約定手数料が上限を超えない場合 \( l_{n(sell)} < l_{max} \)
ETFのパラメータ
調整後一括投資金額
\tilde{t}_0=
\begin{cases}
\displaystyle
\tilde{t}_0= (1-f)t_0-l_{max} & ( l_0 \geq l_{max} ) \\
\displaystyle
\tilde{t}_0=(1-f)(1-l)t_0 & ( l_0 < l_{max} )
\end{cases}
\]
調整後積立金額
\begin{cases}
\displaystyle
(1-f)t-l_{max} & ( l_1 \geq l_{max} ) \\
\displaystyle
(1-f)(1-l)t& ( l_1 < l_{max} < l_nまたは l_n \leq l_{max} )
\end{cases}
\]
調整後配当率
\tilde{d}=
\begin{cases}
\displaystyle
d(1-\tau_{US})(1-\tau_{JP}) & ( l_1 \geq l_{max} ) \\
\displaystyle
d(1-\tau_{US})(1-\tau_{JP})(1-l_{buy})& ( l_1 < l_{max} < l_nまたは l_n \leq l_{max} )
\end{cases}
\]
調整後騰落率
R=\lambda + \tilde{d}
\]
ETFの公式
ETFの公式は以下のようになります。
期初評価額
A_n=\eta_n \tilde{t}_0 + \gamma_n \tilde{t}
\]
投資元本合計
T_n=t_0+nt
\]
期末評価額
M_n=\lambda A_n
\]
期初評価額合計
Z_n=\sum_{k=1}^{n}A_k=\gamma_n \tilde{t}_0 + \mu_n \tilde{t}
\]
キャピタル益合計
C_n=r Z_n
\]
ファンド経費合計
E_n=e(C_n + Z_n)
\]
配当金額合計
D_n=d Z_n
\]
配当金にかかる税金(米国)合計
Q_{n(US)}=\tau_{US} D_n
\end{align}
配当金にかかる税金(国内)合計
Q_{n(JP)}=(1-\tau_{US})\tau_{JP} D_n
\end{align}
配当金にかかる税金(米国、日本)合計
Q_{n}=Q_{n(US)}+Q_{n(JP)}
\end{align}
購入金額合計
W_n=(1-f) T_n + d(1-\tau_{US})(1-\tau_{JP})(Z_n – A_n)-L_n
\]
株式売却にかかる税金合計
U_n=\tau_{JP}(M_n-W_n)
\end{align}
最終受取金額
P_n = M_n+v_n+Q_{n(US)}-H_n-J_n-U_n
\]
トータル実質利回り
R_n=\frac{P_n}{T_n}
\]
購入時為替手数料合計
F_n = fT_n
\]
売却時為替手数料合計
J_n = f (M_n + v_n)
\]
購入時約定手数料 (一括投資分)
L_{0}=
\begin{cases}
\displaystyle
l_{max} & (l_0 \geq l_{max}) \\
\displaystyle
(1-f) l_{buy} t_0& (l_0 < l_{max})
\end{cases}
\]
購入時約定手数料 (積立分)合計
L_{1 \sim n}=
\begin{cases}
\displaystyle
n l_{max} & \left( l_1 \geq l_{max}\right)\\
\displaystyle
(1-f) l_{buy} n t + d l (1-\tau_{US})(1-\tau_{JP}) (Z_n – A_n)& \left( l_1 < l_{max} < l_n または l_n \leq l_{max} \right)
\end{cases}
\]
購入時約定手数料 (一括投資分+積立分)合計
L_n=L_0+L_{1 \sim n}
\]
売却時約定手数料
H_{n}=
\begin{cases}
\displaystyle
l_{max} & \left( l_{n(sell)} \geq l_{max} \right)\\
\displaystyle
l_{sell} M_n & \left( l_{n(sell)} < l_{max} \right)
\end{cases}
\]
最終月に受取る課税後配当金
v_n = (1-\tau_{US})(1-\tau_{JP}) d A_n
\]
ETFの公式(配当金を再投資しない場合)
配当金を再投資しない場合、ETFの公式の一部を以下のように変えることで計算出来ます。
調整後騰落率
R=\lambda
\]
購入金額合計
W_n=(1-f) T_n -L_n
\]
購入時約定手数料 (積立分)合計
L_{1 \sim n}=
\begin{cases}
\displaystyle
n l_{max} & \left( l_1 \geq l_{max}\right)\\
\displaystyle
(1-f) l_{buy} n t & \left( l_1 < l_{max} < l_n または l_n \leq l_{max} \right)
\end{cases}
\]
S&P500指数における比較例
実際にS&P500に連動するETFと投資信託でトータルパフォーマンスを比較してみます。ETFはVOO、投資信託はeMAXIS Slim米国株式 (S&P500)を採用します。
投資計画パラメータ
投資は、以下の条件で行うものとします。
| パラメータ | 意味 | 値 |
|---|---|---|
| \(t_0\) | 一括投資金額[単位:円] | 0 |
| \(t\) | 積立金額[単位:円] | 100,000 |
| \(n\) | 積立月数 | 240 |
ファンドパラメータ
株価上昇率[月]
一般的に、\(N\)ヶ月間で株価が\(p_1\)から\(p_N\)まで上昇した場合、騰落率[月]\(r\)は以下で求められます。
\frac{p_N}{p_1}&=r^N \\
r&=\left(\frac{p_N}{p_1}\right)^{\frac{1}{N}}
\end{align}
S&P500指数SPYは、2008年8月終値で、128.79ドル、2020年7月6日時点で317.05ドルです。期間は約12年間(約60ヶ月)ですので、騰落率[月] \(r\)は以下のようになります。
r=1.006275695
\]
配当率[月]
S&P500指数の直近の年間配当率は\(1.89\%\)ですので配当率[月]\(d\)は以下で求められます。
d=\frac{0.0189}{12}=0.001575
\]
ファンド経費率[月]
VOOのファンド経費率[年]は0.03%、eMAXIS Slim米国株式 (S&P500)のファンド経費率[年]は0.163%です。従って、VOOとeMAXIS Slim米国株式 (S&P500)の月間ファンド経費率はそれぞれ12で割ることで算出出来ます。
まとめると、ファンドパラメータは以下のようになります。
| パラメータ | 意味 | 値 |
|---|---|---|
| \(r\) | 騰落率[月] | 1.006276 |
| \(d\) | 配当率[月] | 0.001575 |
| \(e\) | ファンド経費率[月](ETF) | 0.000025 |
| ファンド経費率[月](投資信託) | 0.000136 |
税金パラメータ
| パラメータ | 意味 | 値 |
|---|---|---|
| \(\tau_{JP}\) | 日本国内税率 | 0.20315 |
| \(\tau_{US}\) | 米国税率 | 0.10000 |
ETF手数料パラメータ
| パラメータ | 意味 | 値 |
|---|---|---|
| \(l_{buy}\) | 購入時約定手数料率 | 0.00495 |
| \(l_{sell}\) | 売却時約定手数料率 | 0.00495 |
| \(l_{max}\) | 約定手数料上限[単位:円] | (*1) 2,354 |
| \(g\) | 為替レート[単位:円/ドル] | 107 |
| \(\epsilon\) | 為替手数料率[単位:円/ドル] | 0.04 |
(*1) 手数料率22ドル(税込)を為替レート107円/ドルで計算
投資信託とETFの最終実質利回りの比較
上述の公式を用いて算出した結果は以下の通りです。この前提においては、VOOの最終実質利回りは\(246.9\%\), eMAXIS Slim 米国株式(S&P500)のトータルパフォーマンスは\(245.4\%\)となり、VOOの方が若干ですがパフォーマンスは優先します。
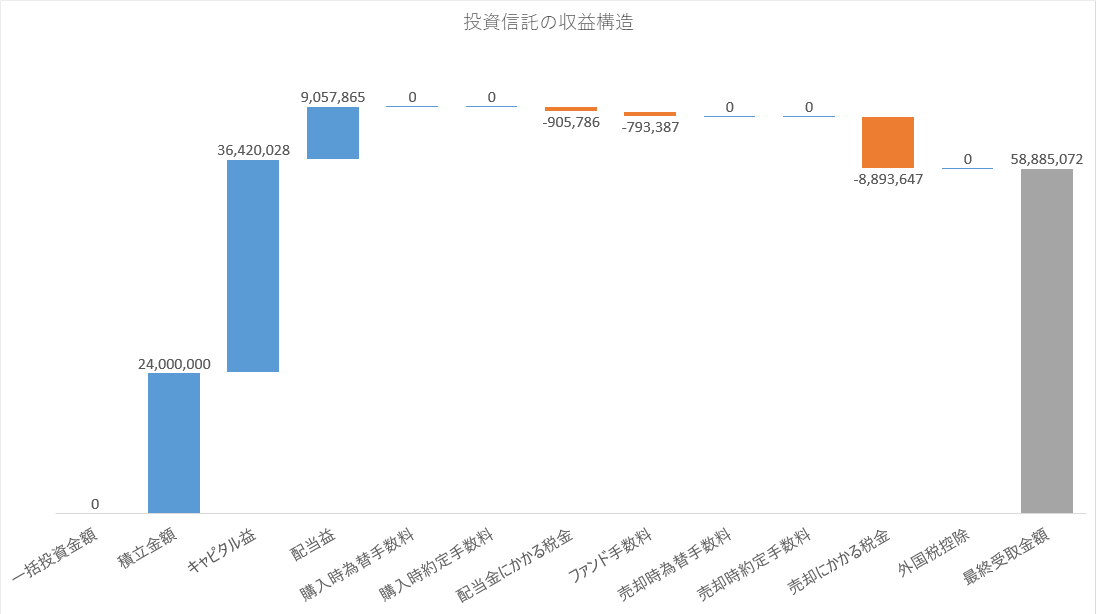
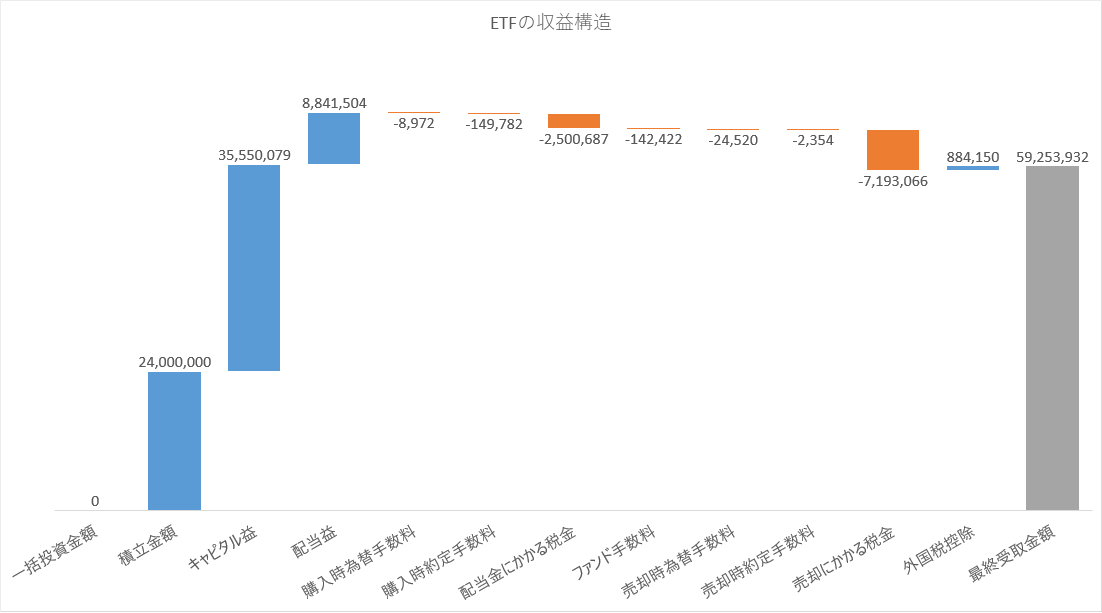
投資信託とETFの収益構造
投資信託の収益構造
最も大きいコストは売却にかかる税金です。次に大きいのは配当金にかかる税金です。最後に大きいのがファンド手数料です。
ETFの収益構造
最も大きいコストは、売却にかかる税金です。次に大きいのはは秘湯金にかかる税金です。約定手数料や為替手数料等は、ほとんどが誤差であることが分かります。
参考:投資期間40年での比較結果
投資期間を40年間に変更して結果を比較してみます。その他の投資条件は前回と同じです。結果は逆転し、投資信託のパフォーマンスがETFを優先します。
直感に反して、投資期間が20年ではVOOが優先し、40年ではETFが優先しました。その理由はなぜでしょうか。理由は、こちらの記事で解説しています。

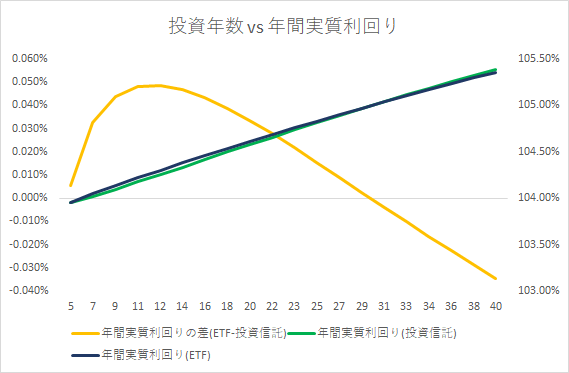
参考:投資年数による年間実質利回りの差
積立期間を5年から40年間まで2年毎に変化させ、その年間実質利回りの差をプロットしてみます。すると、以下のように約30年間の間はETFが投資信託のパフォーマンスを優先しますが、30年以降は投資信託のパフォーマンスがETFを優先します。
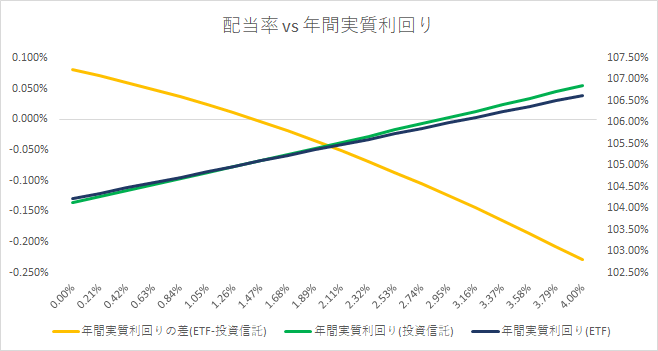
以下は、5万円を50年間VOOとeMAXIS Slimに投資した結果ですが、配当利回りのみを0%から4%で変化させたケースです。配当金が小さい場合は、ETFが有利ですが、配当金が大きい場合は投資信託が有利になることが分かります。配当率1.47%周辺がしきい値であることが分かります。
本公式を用いることで、このようなマニアックなシミュレーションが、Excelの算出式だけで比較的簡単に解析できるのが公式を使ったメリットです。
まとめ
いかがだったでしょうか。少しマニアックな内容になってしまいました。本ページで紹介している数理モデルと公式を用いることで、任意の投資信託やETFの手数料や税金を加味したトータルパフォーマンスを比較することが可能になります。
また、これらの方法は数値計算によってももちろん、同じ結果を導くことが出来ます。